Jak rozwiązywać matematyczne równania z nawiasami

Kolejność wykonywania działań w zadaniach matematycznych często sprawia problemy. Sytuacja komplikuje się jeszcze bardziej, gdy występują nawiasy, które zmieniają kolejność działań.

Kolejność działań w wyrażeniach bez nawiasów

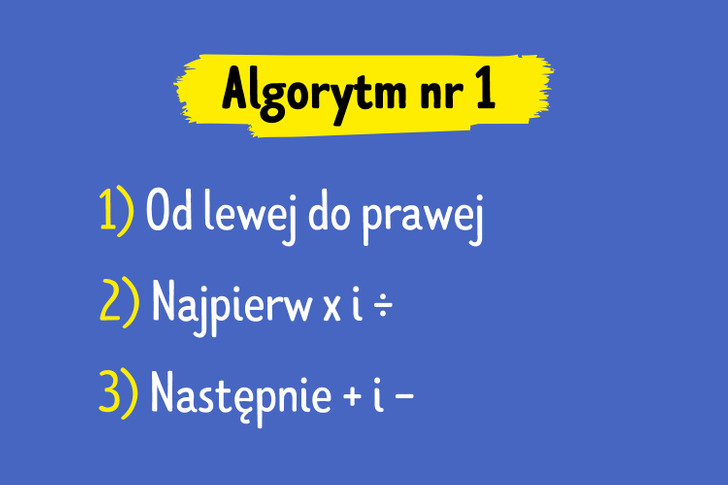
Aby rozwiązywać proste zadania bez nawiasów, obliczać pierwiastki i ułamki, należy pamiętać o poniższych zasadach:

• Wszystkie działania wykonujemy od lewej do prawej.
• Najpierw należy wykonać mnożenie i dzielenie, a następnie dodawanie i odejmowanie.

Jak korzystać z tych zasad?

Przykład nr 1. Oblicz: 15 — 3 + 7.

Najpierw wykonaj wszystkie działania od lewej do prawej:

1) 15 — 3 = 12

2) 12 + 7 = 19

Odpowiedź: 15 — 3 + 7 = 19.

Przykład nr 2. Oblicz: 10 ÷ 2 × 8.

Tu również wykonujemy działania od lewej do prawej:

1) 10 ÷ 2 = 5

2) 5 × 8 = 40

Odpowiedź: 10 ÷ 2 × 8 = 40.

Przykład nr 3. Oblicz: 5 × 4 — 8 ÷ 2.

Również dokonaj obliczeń od lewej do prawej, ale pamiętaj, że mnożenie i dzielenie wykonuje się jako pierwsze. A zatem:

1) 5 × 4 = 20. To jest mnożenie, które występuje jako pierwsze, patrząc od lewej do prawej.

2) 8 ÷ 2 = 4. Jest to dzielenie i mimo że następuje po odejmowaniu, ma ono pierwszeństwo.

3) 20 — 4 = 16. Teraz zwykła kolejność: po mnożeniu i dzieleniu przechodzimy do odejmowania.

Odpowiedź: 5 × 4 — 8 ÷ 2 = 16.

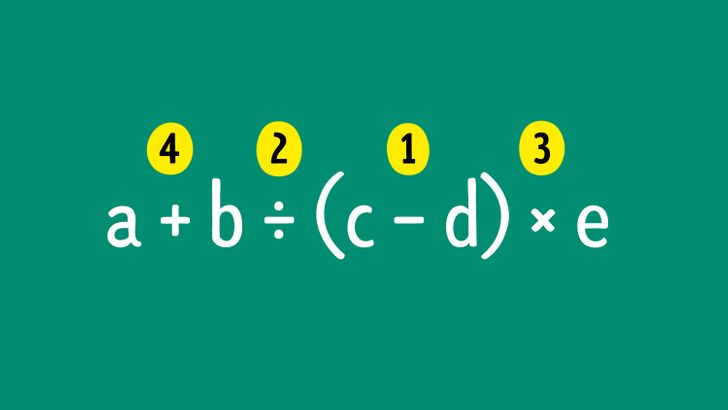
Jeśli masz do wykonania kilka działań, możesz je ponumerować, aż zapamiętasz właściwą kolejność.

Ważne: Nie ma potrzeby umieszczania nawiasów, jeśli dodawanie i odejmowanie wykonuje się od lewej do prawej. Na przykład, zamiast (4 — 2) + 3, można po prostu napisać 4 — 2 + 3. Nie ma również potrzeby stosowania nawiasów, gdy działania i tak są traktowane priorytetowo. Na przykład zamiast 5 + (4 × 3), można po prostu napisać 5 + 4 × 3, ponieważ mnożenie i tak ma pierwszeństwo.

Kolejność wykonywania działań w zadaniach z nawiasami

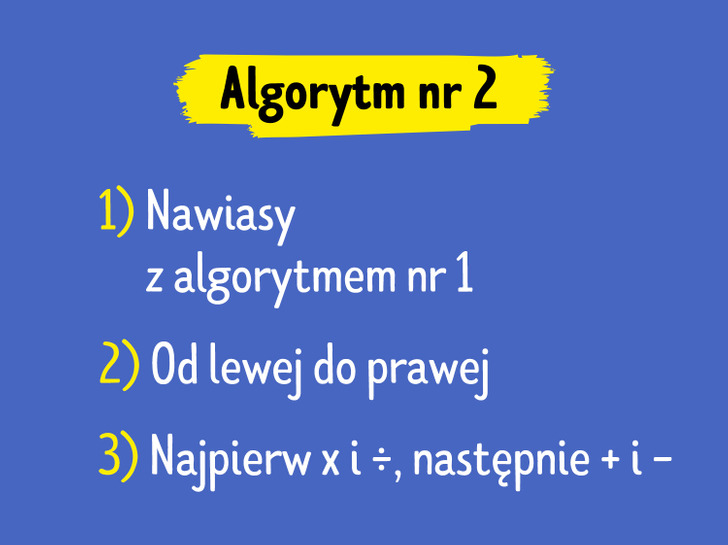
Wyrażenie matematyczne może zawierać nawiasy, które zmieniają zwykłą kolejność wykonywania działań. Aby dokonać właściwych obliczeń, należy pamiętać o następujących zasadach:

• Najpierw wykonuje się wszystkie działania w nawiasach.
• Następnie należy wykonać pozostałe działania od lewej do prawej.
• Mnożenie i dzielenie zawsze wykonuje się jako pierwsze, a następnie odejmowanie i dodawanie.
• Te same zasady dotyczą nawiasów.
• Jeśli występują ułamki lub potęgowanie, należy je obliczyć (jeśli to możliwe) przed wszystkimi innymi operacjami.

Jak korzystać z tych zasad?

Przykład nr 1. Oblicz: 5 × (8 — 4) ÷ 2.

Najpierw wykonaj działania w nawiasach, a następnie postępuj zgodnie ze zwykłą kolejnością:

1) 8 — 4 = 4

Znając wynik w nawiasach, można zapisać 5 × (8 — 4) ÷ 2 = 5 × 4 ÷ 2. Następnie postępuj zgodnie z kolejnością:

2) 5 × 4 = 20

3) 20 ÷ 2 = 10

Zatem 5 × (8 — 4) ÷ 2 = 10.

Odpowiedź: 5 × (8 — 4) ÷ 2 = 10.

Przykład nr 2. Oblicz i porównaj wyniki: 7 — 3 + 2 i 7 — (3 + 2).

Oblicz wynik pierwszego wyrażenia: 7 — 3 + 2 = 6. Teraz oblicz wynik drugiego wyrażenia: 7 — (3 + 2) = 7 — 5 = 2. Nawiasy w drugim przykładzie zmieniły kolejność wykonywania działań, dlatego wyniki są różne.

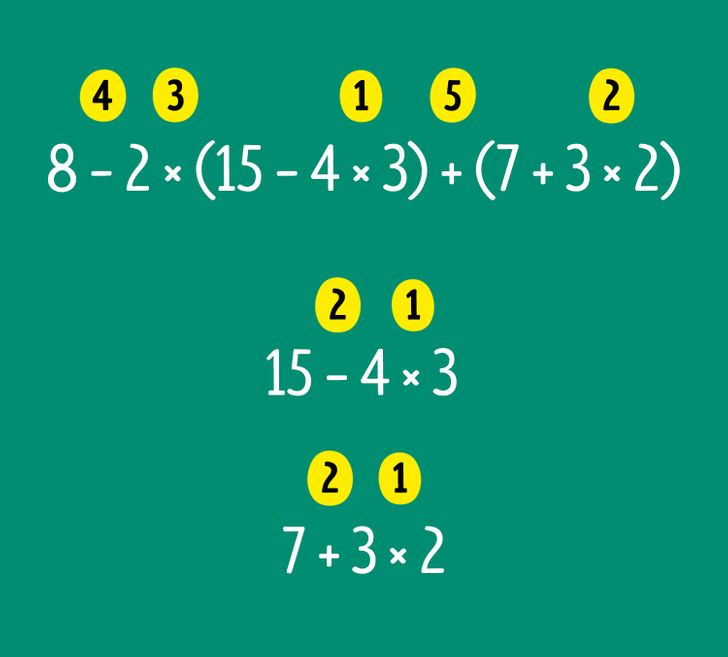
Przykład nr 3. Oblicz 8 — 2 × (15 — 4 × 3) + (7 + 3 × 2).

Na pierwszy rzut oka to wyrażenie wydaje się skomplikowane. Aby uprościć proces, podziel go na osobne działania:

1) Najpierw wykonaj działania w nawiasach. Aby uzyskać prawidłowy wynik w pierwszym nawiasie, należy pamiętać o działaniach, które są priorytetem. Najpierw należy więc obliczyć 4 × 3, a następnie odjąć wynik od 15. Odpowiedź to 3. To samo należy zrobić z drugim nawiasem — oblicz 3 × 2 i dodaj 7. Wynik to 13.

2) Teraz zapisz 8 — 2 × 3 + 13. Wykonaj mnożenie, a następnie odejmowanie i dodawanie: 8 — 6 + 13 = 2 +13 = 15. Odpowiedź: 8 — 2 × (15 — 4 × 3) + (7 + 3 × 2) = 15.

Ważne: Można się czasem natknąć na wyrażenia, w których nawiasy znajdują się wewnątrz innych nawiasów. Zasada jest taka sama: najpierw oblicza się wszystko, co znajduje się w nawiasie wewnętrznym, potem zewnętrznym, a następnie wykonuje się resztę obliczeń. Stosuje się różne nawiasy — w większości przypadków jest to ( ), ale można również użyć { } i [ ].

Skąd wynikają błędy w obliczeniach wyrażeń z nawiasami

• Symbol mnożenia pomija się przed nawiasami, co może prowadzić do pomyłek.

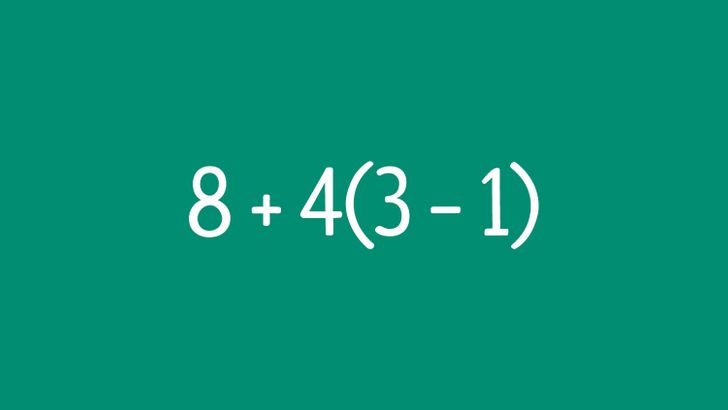
Mamy na przykład takie wyrażenie: 8 + 4(3 — 1). Podczas rozwiązywania tego zadania łatwo jest pomylić kolejność. Prawidłowa kolejność jest następująca: najpierw oblicza się wynik w nawiasie, następnie należy pomnożyć go przez 4 i dodać wynik do 8. Otrzymujemy więc: 8 + 4(3 — 1) = 8 + 4 × (3 — 1) = 8 + 4 × 2 = 8 + 8 = 16.

W tym przypadku sprawy wydają się bardziej skomplikowane: 8 ÷ 4(3 — 1). Ale kolejność jest taka sama. Najpierw nawiasy, a następnie dzielenie i mnożenie od lewej do prawej: 8 ÷ 4 × (3 — 1) = 8 ÷ 4 × 2 = 2 × 2 = 4.

• Nieprawidłowe usuwanie nawiasów z poprzedzającym je minusem

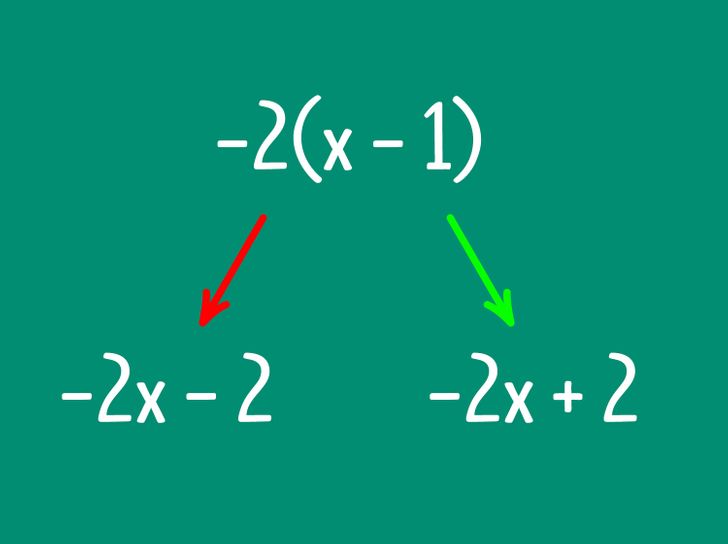
Zdarza się, że w niektórych wyrażeniach należy usunąć nawiasy, żeby je uprościć. W takim przypadku, jeśli przed nawiasem znajduje się minus, wszystkie plusy i minusy należy zastąpić ich przeciwieństwami. Na przykład: 6 + 5 — (4 + 3 — 2) zamienia się w 6 + 5 — 4 — 3 + 2. Bardzo często ludzie popełniają błędy, gdy mają do czynienia ze zmiennymi i złożonymi równaniami, takimi jak 3 + 2(x + 1) — 2(x — 1). Ponieważ nie znamy zmiennej, nie możemy obliczyć wyniku w nawiasach, więc musimy usunąć nawiasy i przekształcić wyrażenie w 3 + 2х + 2 — 2х + 2 = 7. Jeśli popełnisz błąd, będzie to wyglądać następująco: 3 + 2х + 2 — 2х — 2 = 3.

• Obliczenia wykonywane na kalkulatorze

Nie wszystkie kalkulatory potrafią wykonywać działania w prawidłowej kolejności, chociaż niektóre modele odróżniają proste operacje od skomplikowanych. Jak sprawdzić swój kalkulator? Spróbuj obliczyć 1 + 5 × 7. Jeśli uzyskałeś wynik 36, twój kalkulator potrafi rozwiązywać skomplikowane wyrażenia.